Potenzgerade

Unter der Potenzgeraden (Potenzlinie, Chordale) zweier Kreise versteht man den geometrischen Ort (die Menge) aller Punkte, deren Potenz in Bezug auf die beiden Kreise übereinstimmt. Sind die Kreise ${\displaystyle k_{1},k_{2}}$ durch ihre Mittelpunkte ${\displaystyle M_{1}}$ und ${\displaystyle M_{2}}$ sowie ihre Radien ${\displaystyle r_{1}}$ und ${\displaystyle r_{2}}$ gegeben, so sind die Potenzen eines Punktes ${\displaystyle P}$ bezgl. der beiden Kreise

${\displaystyle \Pi _{1}(P)=|PM_{1}|^{2}-r_{1}^{2},\qquad \Pi _{2}(P)=|PM_{2}|^{2}-r_{2}^{2}}$

Ein Punkt ${\displaystyle P}$ gehört zur Potenzgerade ${\displaystyle g_{12}}$, wenn

${\displaystyle \Pi _{1}(P)=\Pi _{2}(P)\ }$ gilt.

Die Potenzgerade ist nur definiert, wenn die gegebenen Kreise nicht konzentrisch sind, also keinen übereinstimmenden Mittelpunkt haben. Sind beide Radien gleich oder sogar 0, so ist die Potenzgerade die Mittelsenkrechte der Punkte ${\displaystyle M_{1},M_{2}}$.

Potenzgeraden spielen bei Kreisbüscheln eine wichtige Rolle: Ein Kreisbüschel ist eine Schar von Kreisen mit einer gemeinsamen Potenzgerade.^[1]

Bezeichnungen:
J. Steiner nannte die Potenzgerade Linie der gleichen Potenzen.^[2]
J.V. Poncelet verwandte chorde ideale.^[3]
J. Plücker führte die Bezeichnung Chordale ein.^[4]
M. Chasles bezeichnet sie als axe radical, was auch im Englischen (radical axis) üblich ist.^[5]
O. Hesse nennt die Potenzgerade gemeinschaftliche Sekante, auch in dem Fall, dass die beiden Kreise keine (reellen) Punkte gemeinsam haben.^[6]

Im Folgenden sind ${\displaystyle {\vec {x}},{\vec {m}}_{1},{\vec {m}}_{2}}$ die Ortsvektoren der Punkte ${\displaystyle P,M_{1},M_{2}}$. Die definierende Gleichung der Potenzgerade lässt sich damit schreiben:

${\displaystyle ({\vec {x}}-{\vec {m}}_{1})^{2}-r_{1}^{2}=({\vec {x}}-{\vec {m}}_{2})^{2}-r_{2}^{2}\quad \leftrightarrow \quad 2{\vec {x}}\cdot ({\vec {m}}_{2}-{\vec {m}}_{1})+{\vec {m}}_{1}^{2}-{\vec {m}}_{2}^{2}+r_{2}^{2}-r_{1}^{2}=0}$

Aus der rechten Gleichung erkennt man

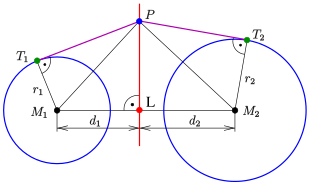
• Die als Potenzgerade definierte Punktmenge ist tatsächlich eine Gerade und steht senkrecht auf der Verbindungsgerade der Mittelpunkte. (${\displaystyle {\vec {m}}_{2}-{\vec {m}}_{1}}$ ist eine Normale der Potenzgerade!)

Dividiert man die Gleichung durch ${\displaystyle 2|{\vec {m}}_{2}-{\vec {m}}_{1}|}$, erhält man die Hessesche Normalenform. Einsetzen der Mittelpunkte liefert die Abstände der Potenzgerade zu den Mittelpunkten:

${\displaystyle d_{1}={\frac {d^{2}+{r_{1}}^{2}-{r_{2}}^{2}}{2d}}\ ,\qquad d_{2}={\frac {d^{2}+{r_{2}}^{2}-{r_{1}}^{2}}{2d}}}$.

Dabei ist ${\displaystyle d=|M_{1}M_{2}|}$.

(Bei Verwendung der äquivalenten linken Gleichung in der Form ${\displaystyle \cdots =0}$ wird die Berechnung von ${\displaystyle d_{1},d_{2}}$ besonders einfach.)

Schneiden sich die beiden Kreise, so geht die Potenzgerade durch die gemeinsamen Punkte. Falls sie sich nur berühren ist die gemeinsame Tangente die Potenzgerade.

• Für zwei sich schneidende Kreise (Fall 3) geht die Potenzgerade durch die beiden Schnittpunkte. Falls sich die beiden Kreise berühren (Fall 2 und Fall 4), stimmt die Potenzgerade mit der gemeinsamen Tangente überein.

• Für die Punkte der Potenzgeraden, die außerhalb der gegebenen Kreise liegen, sind die Tangentenabschnitte an beide Kreise gleich lang (siehe den Artikel über Potenz). Sind ${\displaystyle S_{1},T_{1},S_{2},T_{2}}$ die Berührpunkte der Tangenten durch ${\displaystyle P}$ an die beiden Kreise, so liegen ${\displaystyle S_{1},T_{1},S_{2},T_{2}}$ auf einem die Kreise ${\displaystyle k_{1},k_{2}}$ senkrecht schneidenden Kreis ${\displaystyle k_{o}}$.
• Die Potenzgerade zweier Kreise ist die Menge der Mittelpunkte aller Kreise, welche die gegebenen Kreise rechtwinklig schneiden.

Die im vorigen Abschnitt enthaltene Möglichkeit zu zwei Kreisen ein System von Kreisen zu konstruieren, die die gegebenen Kreise orthogonal schneiden, lässt sich zu einer Konstruktion von zwei Systemen von Kreisen, die sich orthogonal schneiden^[7][8], ausbauen:

Es seien ${\displaystyle k_{1},k_{2}}$ zwei getrennt liegende Kreise (wie im vorigen Abschnitt), ${\displaystyle M_{1},M_{2},r_{1},r_{2}}$ deren Mittelpunkte und Radien und ${\displaystyle g_{12}}$ deren Potenzgerade. Es werden nun diejenigen Kreise gesucht, deren Mittelpunkte auf der Gerade ${\displaystyle {\overline {M_{1}M_{2}}}}$ liegen und deren Potenzgerade zusammen mit ${\displaystyle k_{1}}$ auch ${\displaystyle g_{12}}$ ist. Es sei ${\displaystyle \kappa _{2}}$ ein solcher Kreis, dessen Mittelpunkt von ${\displaystyle M_{1}}$ den Abstand ${\displaystyle \delta }$ und den Radius ${\displaystyle \rho _{2}}$ hat. Nach dem Resultat des vorigen Abschnitts ist dann

${\displaystyle d_{1}={\frac {\delta ^{2}+r_{1}^{2}-\rho _{2}^{2}}{2\delta }}\quad }$, wobei ${\displaystyle d_{1}>r_{1}}$ fest sind.

Mit ${\displaystyle \delta _{2}=\delta -d_{1}}$ lässt sich diese Gleichung umformen zu:

${\displaystyle \delta _{2}^{2}=d_{1}^{2}-r_{1}^{2}+\rho _{2}^{2}}$.

Gibt man den Radius ${\displaystyle \rho _{2}}$ vor, ergibt sich aus dieser Gleichung der Abstand ${\displaystyle \delta _{2}}$ des neuen Mittelpunktes von der (festen) Potenzgerade. In der Abbildung sind die neuen Kreise lila. Die grünen Kreise (siehe Abbildung) mit Mittelpunkte auf der Potenzgerade schneiden ${\displaystyle k_{1},k_{2}}$ senkrecht und damit auch alle neuen Kreise (lila). Wenn man die (rote) Potenzgerade als y-Achse und ${\displaystyle {\overline {M_{1}M_{2}}}}$ als x-Achse wählt, haben die beiden Kreisscharen die folgenden Gleichungen:

lila: ${\displaystyle \ \ \ (x-\delta _{2})^{2}+y^{2}=\delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}}$

grün: ${\displaystyle \ x^{2}+(y-y_{g})^{2}=y_{g}^{2}+d_{1}^{2}-r_{1}^{2}\ .}$

(${\displaystyle \;(0,y_{g})}$ ist der Mittelpunkt eines grünen Kreises.)

Eigenschaften:
a) Die grünen Kreise schneiden sich alle auf der x-Achse in den beiden Punkten ${\displaystyle P_{1/2}={\big (}\pm {\sqrt {d_{1}^{2}-r_{1}^{2}}},0{\big )}}$, den Polen des orthogonalen Kreissystems, d. h. die x-Achse ist die Potenzgerade der grünen Kreise.
b) Die lila Kreise haben keine (reellen) Punkte gemeinsam. Fasst man aber die reelle Ebene als Teil der komplexen Ebene auf, so schneiden sich die lila Kreise auf der y-Achse (gemeinsame Potenzgerade) in den beiden Punkten ${\displaystyle Q_{1/2}={\big (}0,\pm i{\sqrt {d_{1}^{2}-r_{1}^{2}}}{\big )}}$.

Sonderfälle:
a) Im Fall ${\displaystyle d_{1}=r_{1}}$ berühren sich sowohl die grünen als auch die lila Kreise im Nullpunkt. Sie bilden zwei sich orthogonal schneidende parabolische Kreisbüschel (siehe unten).
b) Lässt man ${\displaystyle k_{1}}$ auf den Punkt ${\displaystyle M_{1}}$ schrumpfen, d. h. ${\displaystyle r_{1}=0}$, so vereinfachen sich die Gleichungen und es ist ${\displaystyle M_{1}=P_{1}}$.

Zusammenfassung:
a) Für jede reelle Zahl ${\displaystyle c}$ gilt für die Kreisschar

${\displaystyle \;k(\xi ):\;(x-\xi )^{2}+y^{2}-\xi ^{2}-c=0\ :}$

Je zwei Kreise ${\displaystyle k(\xi _{1}),k(\xi _{2})}$ haben die y-Achse als Potenzgerade.

Für ${\displaystyle c>0}$ schneiden sich ${\displaystyle k(\xi _{1}),k(\xi _{2})}$ in den Punkten ${\displaystyle P_{1/2}=(0,\pm {\sqrt {c}})}$.

Für ${\displaystyle c<0}$ haben ${\displaystyle k(\xi _{1}),k(\xi _{2})}$ keinen Punkt gemeinsam.

Für ${\displaystyle c=0}$ berühren sich ${\displaystyle k(\xi _{1}),k(\xi _{2})}$ in dem Punkt ${\displaystyle (0,0)}$.

b) Für jede reelle Zahl ${\displaystyle c}$ bilden die beiden Kreisscharen

${\displaystyle k_{1}(\xi ):\;(x-\xi )^{2}+y^{2}-\xi ^{2}-c=0\ ,}$

${\displaystyle k_{2}(\eta ):\;x^{2}+(y-\eta )^{2}-\eta ^{2}+c=0\ }$

ein System orthogonaler Kreise. D.h.: ${\displaystyle k_{1}(\xi ),k_{2}(\eta )}$ schneiden sich für alle ${\displaystyle \xi ,\eta }$ orthogonal.

Für ${\displaystyle c>0}$ sind ${\displaystyle P_{1/2}=(0,\pm {\sqrt {c}})}$ die Pole.

Für ${\displaystyle c<0}$ sind ${\displaystyle P_{1/2}=(\pm {\sqrt {-c}},0)}$ die Pole.

Für ${\displaystyle c=0}$ ist ${\displaystyle P_{1}=P_{2}}$ und das System ist parabolisch.

c) Die Gleichungen in b) lassen sich zur koordinatenfreien Formulierung verwenden:

Sind die beiden Punkte ${\displaystyle P_{1},P_{2}}$ gegeben, ${\displaystyle O}$ ihr Mittelpunkt und ${\displaystyle g_{12}}$ ihre Mittelsenkrechte, so beschreiben die beiden Gleichungen

${\displaystyle |XM|^{2}=|OM|^{2}-|OP_{1}|^{2}\ ,}$

${\displaystyle |XN|^{2}=|ON|^{2}+|OP_{1}|^{2}=|NP_{1}|^{2}}$

mit ${\displaystyle M}$ auf ${\displaystyle {\overline {P_{1}P_{2}}}}$, aber nicht zwischen ${\displaystyle P_{1},P_{2}}$, und ${\displaystyle N}$ auf ${\displaystyle g_{12}}$

das durch ${\displaystyle P_{1},P_{2}}$ eindeutig bestimmte orthogonale System von Kreisen. ${\displaystyle P_{1},P_{2}}$ sind die Pole des Systems.

Für ${\displaystyle P_{1}=P_{2}=O}$ muss man zusätzlich die beiden Potenzgeraden, die Achsen des Systems, ${\displaystyle a_{1},a_{2}}$ vorgeben. Es ergibt sich das parabolische System:

${\displaystyle |XM|^{2}=|OM|^{2}\ ,\quad |XN|^{2}=|ON|^{2}}$

mit ${\displaystyle M}$ auf ${\displaystyle a_{1}}$ und ${\displaystyle N}$ auf ${\displaystyle a_{2}}$.

Konstruktion mit Zirkel und Lineal:

Ein orthogonales Kreissystem ist durch die Vorgabe seiner Pole ${\displaystyle P_{1},P_{2}}$ eindeutig bestimmt:

1. Die Achsen (Potenzgeraden) sind die Gerade ${\displaystyle {\overline {P_{1}P_{2}}}}$ und die Mittelsenkrechte ${\displaystyle g_{12}}$ der Pole.
2. Die Kreise (im Bild grün) durch ${\displaystyle P_{1},P_{2}}$ haben ihre Mittelpunkte auf ${\displaystyle g_{12}}$. Zu einem Punkt ${\displaystyle N}$ ist der Radius ${\displaystyle \;r_{N}=|NP_{1}|\;}$.
3. Um einen Kreis der zweiten Schar (im Bild blau) mit Mittelpunkt ${\displaystyle M}$ auf ${\displaystyle {\overline {P_{1}P_{2}}}}$ zu zeichnen, bestimmt man mit dem Satz des Pythagoras den Radius aus ${\displaystyle \;r_{M}^{2}=|OM|^{2}-|OP_{1}|^{2}\;}$ wie in dem Bild gezeigt.

Falls ${\displaystyle P_{1}=P_{2}}$ ist, müssen die Achsen vorgegeben werden. Das System ist dann parabolisch und leicht zu zeichnen.

Definition und Eigenschaften:

Sind ${\displaystyle k_{1},k_{2}}$ zwei Kreise und ${\displaystyle \Pi _{1},\Pi _{2}}$ ihre Potenzfunktionen, so ist für jedes ${\displaystyle \lambda \neq 1}$

• ${\displaystyle \Pi _{1}(x,y)-\lambda \Pi _{2}(x,y)=0}$

die Gleichung eines Kreises ${\displaystyle k(\lambda )}$ (siehe unten). Diese Schar von Kreisen nennt man das von ${\displaystyle k_{1},k_{2}}$ erzeugte Kreisbüschel.

Die Potenzfunktion von ${\displaystyle k(\lambda )}$ ist

${\displaystyle \ \Pi (\lambda ,x,y)={\frac {\Pi _{1}(x,y)-\lambda \Pi _{2}(x,y)}{1-\lambda }}}$.

Man rechnet leicht nach, dass gilt:

• ${\displaystyle k(\lambda ),k(\mu ),\ \lambda \neq \mu \ ,}$ haben dieselbe Potenzgerade wie ${\displaystyle k_{1},k_{2}}$.

(H): Schneiden sich ${\displaystyle k_{1},k_{2}}$ in zwei Punkten ${\displaystyle P_{1},P_{2}}$, so gehen auch alle Kreise ${\displaystyle k(\lambda )}$ durch ${\displaystyle P_{1},P_{2}}$ und die Gerade ${\displaystyle {\overline {P_{1}P_{2}}}}$ ist ihre gemeinsame Potenzgerade. Ein solches Kreisbüschel heißt elliptisch.
(P): Berühren sich ${\displaystyle k_{1},k_{2}}$ in ${\displaystyle P}$, so berühren sich alle ${\displaystyle k(\lambda )}$ und die gemeinsame Tangente ist die Potenzgerade. Das Kreisbüschel heißt parabolisch.
(E): Haben ${\displaystyle k_{1},k_{2}}$ keinen Punkt gemeinsam, so auch alle Kreise ${\displaystyle k(\lambda )}$ und das Büschel heißt hyperbolisch.

Konkret:

Führt man so Koordinaten ein, dass

${\displaystyle k_{1}:(x-d_{1})^{2}+y^{2}=r_{1}^{2}}$

${\displaystyle k_{2}:(x-d_{2})^{2}+y^{2}=d_{2}^{2}+r_{1}^{2}-d_{1}^{2}}$,

so ist die y-Achse ihre Potenzgerade (siehe oben).

Falls ${\displaystyle r_{1}>d_{1}}$ ist, haben ${\displaystyle k_{1},k_{2},k(\lambda )}$ die beiden Punkte

${\displaystyle P_{1}={\big (}0,{\sqrt {r_{1}^{2}-d_{1}^{2}}}{\big )},\quad P_{2}={\big (}0,-{\sqrt {r_{1}^{2}-d_{1}^{2}}}{\big )}}$

gemeinsam und das Kreisbüschel ist elliptisch.

Falls ${\displaystyle r_{1}=d_{1}}$ ist, haben ${\displaystyle k_{1},k_{2},k(\lambda )}$ den Punkt

${\displaystyle P_{0}=(0,0)}$

gemeinsam und das Büschel ist parabolisch.

Falls ${\displaystyle r_{1}<d_{1}}$ ist, haben ${\displaystyle k_{1},k_{2},k(\lambda )}$ keinen Punkt gemeinsam und das Büschel ist hyperbolisch.

Die Berechnung der Potenzfunktion ${\displaystyle \Pi (\lambda ,x,y)}$ liefert die Gleichung des Kreises:

${\displaystyle k(\lambda ):\ x^{2}+y^{2}-2{\tfrac {d_{1}-\lambda d_{2}}{1-\lambda }}\;x+d_{1}^{2}-r_{1}^{2}=0\ .}$

Quadratische Ergänzung und die Substitution ${\displaystyle \delta _{2}={\tfrac {d_{1}-\lambda d_{2}}{1-\lambda }}}$ (x-Koordinate des Mittelpunktes) führt auf die Mittelpunktsform

${\displaystyle k(\lambda ):\ (x-\delta _{2})^{2}+y^{2}=\delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}}$.

Alternative Formen:
1) In der definierenden Gleichung des Kreisbüschels müssen nicht die Potenzfunktionen selbst stehen. Es können auch jeweils Vielfache davon verwendet werden.
2) Die Gleichung eines der beiden Kreise kann man auch durch die Gleichung der gewünschten Potenzgerade ersetzen. Die Potenzgerade kann man also als einen Kreis mit unendlich großem Radius ansehen. Z.B.:

${\displaystyle {\Big (}(x-x_{1})^{2}+y^{2}-r_{1}^{2}{\Big )}-\lambda \;2(x-x_{2})=0\ \Leftrightarrow }$

${\displaystyle (x-(x_{1}+\lambda ))^{2}+y^{2}=(x_{1}+\lambda )^{2}+r_{1}^{2}-x_{1}^{2}-2\lambda x_{2}}$,

beschreibt alle Kreise, die mit dem ersten Kreis die Gerade ${\displaystyle x=x_{2}}$ als Potenzgerade besitzen.
3) Um beide Kreise in der Definitionsgleichung formal gleich zu behandeln, verwendet man auch gelegentlich die symmetrisierte Form

${\displaystyle \mu \Pi _{1}+\nu \Pi _{2}=0\ }$,

wobei ${\displaystyle \mu ,\nu }$ nicht gleichzeitig Null sein dürfen. Der Nachteil dieser Form: Sie ist bezgl. ${\displaystyle \mu ,\nu }$ nicht eindeutig.

Anwendung:
a) Kreisspiegelungen und Möbiustransformationen sind kreistreue und winkeltreue Abbildungen der Ebene. Orthogonale Kreisbüschel spielen deshalb bei Untersuchungen dieser Abbildungen eine besondere Rolle.^[9][10]
b) In der Elektrodynamik treten Kreisbüschel als Feldlinien auf. Sie werden dort, wie im Englischen (coaxal circles), auch koaxiale Kreise genannt.^[11]

• Sind drei Kreise gegeben, unter denen keine zwei konzentrisch sind, so existieren drei Potenzgeraden (jeweils eine zu zwei Kreisen). Falls die Mittelpunkte der gegebenen Kreise nicht auf einer Geraden liegen, schneiden sich die Potenzgeraden in einem Punkt (engl. radical center), und zwar im Mittelpunkt des Kreises, der die gegebenen Kreise rechtwinklig schneidet (engl. radical circle). Zum Nachweis: die Potenzgerade ${\displaystyle g_{ik}}$ enthält alle Punkte, die vom i-ten und k-ten Kreis denselben tangentialen Abstand haben. Der Schnittpunkt ${\displaystyle R}$ von ${\displaystyle g_{12}}$ und ${\displaystyle g_{23}}$ muss also zu allen drei Kreisen denselben tangentialen Abstand besitzen und damit auch auf ${\displaystyle g_{13}}$ liegen.

Diese Eigenschaft gibt die Möglichkeit die Potenzgerade von zwei sich nicht schneidenden Kreisen ${\displaystyle k_{1},k_{2}}$ zeichnerisch zu bestimmen: Man zeichne einen dritten Kreis ${\displaystyle k_{3}}$, der die gegebenen Kreise schneidet. Damit lassen sich die Potenzgeraden ${\displaystyle g_{13},g_{23}}$ zeichnen. Ihr Schnittpunkt ${\displaystyle R}$ liegt auf ${\displaystyle g_{12}}$, die als Lotgerade von ${\displaystyle R}$ auf die Gerade ${\displaystyle {\overline {M_{1}M_{2}}}}$ gezeichnet werden kann.

Weitere Konstruktion:

Die Punkte, die bezgl. eines Kreises ${\displaystyle k}$ die gleiche Potenz besitzen, liegen auf einem zu ${\displaystyle k}$ konzentrischen Kreis. Diese Eigenschaft lässt sich zu einer weiteren Methode zur Konstruktion der Potenzgerade zweier Kreise verwenden:

Sind zwei sich nicht schneidende Kreise ${\displaystyle k_{1},k_{2}}$ gegeben, so lassen sich, wie in der Zeichnung gezeigt, zu jedem Kreis ${\displaystyle k_{i}}$ ein weiterer Kreis ${\displaystyle c_{i}}$ zeichnen, mit der Eigenschaft: Die Punkte der Kreise ${\displaystyle c_{1},c_{2}}$ haben bezüglich der Kreise ${\displaystyle k_{1},k_{2}}$ die gleiche Potenz. Formal: ${\displaystyle \Pi _{1}(P_{1})=\Pi _{2}(P_{2})}$. Ist die Potenz groß genug gewählt, schneiden sich ${\displaystyle c_{1},c_{2}}$ und liefern zwei Punkte der gesuchten Potenzgerade der Kreise ${\displaystyle k_{1},k_{2}}$.

Falls die Radien der beiden Kreise Null sind, ist die Potenzgerade die Mittelsenkrechte von ${\displaystyle M_{1},M_{2}}$ und die Konstruktion ist die für Mittelsenkrechte übliche.

1. ↑ G. Aumann: Kreisgeometrie, S. 45
2. ↑ Jakob Steiner: Einige geometrische Betrachtungen. In: Journal für die reine und angewandte Mathematik, Band 1, 1826, S. 165
3. ↑ Ph. Fischer: Lehrbuch der analytische Geometrie, Darmstadt 1851, Verlag Ernst Kern, p. 67
4. ↑ H. Schwarz: Die Elemente der analytischen Geometrie der Ebene, Verlag H. W. Schmidt, Halle, 1858, S. 218
5. ↑ Michel Chasles, C. H. Schnuse: Die Grundlehren der neuern Geometrie, erster Theil, Verlag Leibrock, Braunschweig, 1856, S. 312
6. ↑ O. Hesse: Analytische Geometrie der geraden Linie, des Punktes und des Kreises in der Ebene, Teubner-Verlag, Leipzig, 1881, S. 195.
7. ↑ A. Schoenflies, R. Courant: Einführung in die Analytische Geometrie der Ebene und des Raumes, Springer-Verlag, 1931, S. 113
8. ↑ C. Caratheodory: Funktionentheorie, Birkhäuser-Verlag, Basel, 1961, ISBN 978-3-7643-0064-7, S. 46
9. ↑ Caratheodory: Funktionentheorie, S, 47.
10. ↑ R. Sauer: Ingenieur-Mathematik: Zweiter Band: Differentialgleichungen und Funktionentheorie, Springer-Verlag, 1962, ISBN 978-3-642-53232-0, S. 105
11. ↑ Clemens Schaefer: Elektrodynamik und Optik, Verlag: De Gruyter, 1950, ISBN 978-3-11-230936-0, S. 358.

• Günter Aumann: Kreisgeometrie, Springer Spektrum, 2015, ISBN 978-3-662-45305-6, S. 39
• Max Koecher, Aloys Krieg: Ebene Geometrie. Springer, 2013, ISBN 978-3-662-06809-0, S. 138–140
• Harald Scheid, Wolfgang Schwarz: Elemente der Geometrie. Springer, 2016, ISBN 978-3-662-50323-2, S. 156–158

• Eric W. Weisstein: Radical line. In: MathWorld (englisch).
• Geogebra: Potenzgeraden interaktiv