Takagi-Funktion

Die Takagi-Funktion (auch bekannt als Blancmange-Funktion) ist eine reellwertige Funktion einer reellen Variablen. Sie ist eine auf dem gesamten Definitionsbereich stetige, aber nicht differenzierbare Funktion.^[1]

Die Funktion wurde ursprünglich vom japanischen Mathematiker Takagi Teiji im Jahr 1903 als Beispiel einer stetigen und nirgends differenzierbaren Funktion angegeben.^[2] Andere Beispiele derartiger Funktionen hatten im 19. Jahrhundert bereits Karl Weierstraß und Bernard Bolzano gefunden.^[1] Anfangs fand die Funktion unter westlichen Mathematikern wenig Beachtung. Im Jahr 1930 publizierte der Niederländer van der Waerden eine ähnliche Funktion mit der Basis zehn statt zwei. Neun Jahre später griff der norwegische Mathematiker Tambs-Lyche die Takagi-Funktion als ein für beginnende Mathematikstudenten zugängliches Beispiel einer stetigen und nirgends differenzierbaren Funktion wieder auf.^[3] Die Funktion ist aufgrund der Ähnlichkeit ihres Graphen mit der Süßspeise Mandelsulz (französisch: blanc-manger) auch als Blancmange-Funktion bekannt.^[4]

Die Takagi-Funktion ist definiert als

${\displaystyle T\colon [0,1]\to \mathbb {R} ,\;x\mapsto \sum _{n=0}^{\infty }{\frac {\phi (2^{n}x)}{2^{n}}}}$,

wobei ${\displaystyle \textstyle \phi (x):=\min _{k\in {\mathbb {Z} }}|x-k|}$ der Abstand von ${\displaystyle x}$ zur nächsten ganzen Zahl ist.

Takagi stellte die Funktion ursprünglich leicht anders dar.^[3] Der Definitionsbereich lässt sich periodisch auf ganz ${\displaystyle \mathbb {R} }$ erweitern.

Die Takagi-Funktion ist wohldefiniert, da für alle ${\displaystyle x\in [0,1]}$ die Reihe ${\displaystyle \textstyle T(x)=\sum _{n=0}^{\infty }{\phi (2^{n}x) \over 2^{n}}}$ konvergiert. Dies lässt sich zum Beispiel mit dem Weierstraßschem Majorantenkriterium zeigen. Betrachte die Funktionenfolge ${\displaystyle \textstyle (f_{n})_{n\in \mathbb {N} _{0}}}$mit ${\displaystyle \textstyle f_{n}\colon [0,1]\to \mathbb {R} ,\;x\mapsto {\frac {\phi (2^{n}x)}{2^{n}}}}$, für alle ${\displaystyle \textstyle n\in \mathbb {N} _{0}}$. Es gilt für alle ${\displaystyle \textstyle n\in \mathbb {N} _{0}}$, dass ${\displaystyle \textstyle \sup _{x\in [0,1]}f_{n}(x)\leq {\frac {1}{2^{n+1}}}=:M_{n}}$, da ${\displaystyle \textstyle \phi (2^{n}x)\leq {\frac {1}{2}}}$. Zudem gilt ${\displaystyle \textstyle \sum _{n=0}^{\infty }M_{n}={\frac {1}{2}}\sum _{n=0}^{\infty }\left({\frac {1}{2}}\right)^{n}={\frac {\frac {1}{2}}{1-{\frac {1}{2}}}}=1<\infty }$ laut Konvergenz der geometrischen Reihe. Also konvergiert laut Weierstraßschem Majorantenkriterium die Reihe ${\displaystyle \textstyle T(x)=\sum _{n=0}^{\infty }f_{n}(x)=\sum _{n=0}^{\infty }{\phi (2^{n}x) \over 2^{n}}}$ sogar gleichmäßig und absolut.

Die Takagi-Funktion ist stetig. Denn die Partialsummen ${\displaystyle \textstyle \sum _{n=0}^{N}{\phi (2^{n}x) \over 2^{n}}}$ sind für alle ${\displaystyle \textstyle N\in \mathbb {N} _{0}}$ stetige Funktionen und konvergieren, wie oben gezeigt, gleichmäßig gegen die Tagaki-Funktion.

Die Takagi-Funktion ist an keiner Stelle ihres Definitionsbereichs differenzierbar (im Sinne der durch den gewöhnlichen Betrag auf den reellen Zahlen induzierten Topologie).

Beweis (nach Billingsley): Sei ${\displaystyle x\in [0,1]}$ beliebig. Für alle ${\displaystyle k\in \mathbb {N} }$ seien ${\displaystyle a_{k}:=2^{-k}s_{k}}$ und ${\displaystyle b_{k}:=2^{-k}t_{k}}$ mit ${\displaystyle s_{k},t_{k}\in \mathbb {N} }$, sodass gilt ${\displaystyle a_{k}-b_{k}=2^{-k}}$ und ${\displaystyle b_{k}\leq x<a_{k}}$. Sei wie oben ${\displaystyle \textstyle f_{n}\colon [0,1]\to \mathbb {R} ,\;x\mapsto {\frac {\phi (2^{n}x)}{2^{n}}}}$. Dann gilt für den Differenzenquotient:

${\displaystyle {\frac {T(a_{k})-T(b_{k})}{a_{k}-b_{k}}}=\sum _{n=0}^{k-1}{\frac {f_{n}(a_{k})-f_{n}(b_{k})}{a_{k}-b_{k}}}=\sum _{n=0}^{k-1}f_{n}^{+}(x)}$,

wobei ${\displaystyle f_{n}^{+}(x)}$ die rechtsseitige Ableitung von ${\displaystyle f_{n}}$ an der Stelle ${\displaystyle x}$ ist. Die erste Gleichheit stimmt, da ${\displaystyle f_{n}(a_{k})=f_{n}(b_{k})=0}$ für alle ${\displaystyle n\geq k}$ ist. Die zweite Gleichheit folgt hingegen, da ${\displaystyle f_{n}}$ auf dem Intervall ${\displaystyle [b_{k},a_{k}]}$ linear mit Steigung ${\displaystyle f_{n}^{+}(x)}$ ist. Weil aber ${\displaystyle f_{n}^{+}(x)\in \{-1,+1\}}$, kann der Differenzenquotient für ${\displaystyle k\to \infty }$ laut Nullfolgenkriterium nicht konvergieren. Also ist ${\displaystyle T}$ an der Stelle ${\displaystyle x}$ nicht differenzierbar.^[3]

Der Graph der Takagi-Funktion kann anhand der ersten ${\displaystyle N\in \mathbb {N} _{0}}$ Partialsumme der Reihe ${\displaystyle \textstyle T(x)=\sum _{n=0}^{\infty }{\phi (2^{n}x) \over 2^{n}}}$ approximiert werden. Die folgende Grafik illustriert dies für verschiedene Werte von ${\displaystyle N}$. In jedem Schritt werden Dreieckschwingungen mit sich jeweils halbierender Periodenlänge und Höhe (in rot) zum Graph hinzugefügt (was genau dem nächsten Summanden der Reihe entspricht).

${\displaystyle N=0}$	${\displaystyle N=1}$	${\displaystyle N=2}$	${\displaystyle N=3}$

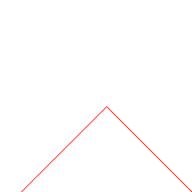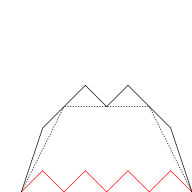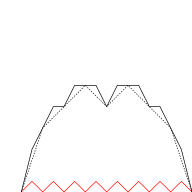Die Takagi-Funktion nimmt ihr Maximum an überabzählbar vielen Punkten mit einem Wert von ${\displaystyle \textstyle {\frac {2}{3}}}$ an.^[3] Ihr Graph ist ein Fraktal und hat eine Hausdorff-Dimension von eins.^[3]

• Weierstraß-Funktion

1. ↑ ^{a b} Konrad Königsberger: Analysis 1. 6. Auflage. Springer, Berlin 2004, ISBN 978-3-540-40371-5, 9.11. 
2. ↑ Teiji Takagi: A Simple Example of the Continuous Function without Derivative. In: Phys.-Math. Soc. Japan. Band 1, 1903, S. 176–177. 
3. ↑ ^{a b c d e} Pieter C. Allaart und Kiko Kawamura: The Takagi Function: a Survey. In: Real Anal. Exchange 37 (2011/12), no. 1, 1-54. Band 37, Nr. 1, 2012, S. 1–54. 
4. ↑ Eric W. Weisstein: Blancmange Function. In: MathWorld-A Wolfram Web Resource. Abgerufen am 26. Juli 2018.