Hasított komplex számok

Hasított-komplex szorzás
× 1 j
1 1 j
j j 1

Az absztrakt algebrában a hasított komplex számok (hiperbolikus számok, perplex számok, kettős számok) a komplex számokhoz hasonlóan valós és képzetes részből állnak, de itt a képzetes egység négyzete nem -1, hanem 1. Jelben z = x + y j , j 2 = + 1. {\displaystyle z=x+yj,\quad j^{2}=+1.} z konjugáltja z* = x - y j. Mivel j2 = +1, z z ∗ = x 2 − y 2 , {\displaystyle zz^{*}=x^{2}-y^{2},} , izotropikus kvadratikus alak, N ( z ) = x 2 − y 2 . {\displaystyle N(z)=x^{2}-y^{2}.}

A hasított komplex számok halmazát D jelöli, ami a szokásos műveletekkel gyűrű a valós számok fölött. Ha w és z hasított komplex számok, akkor szorzatuk eleget tesz az N ( w z ) = N ( w ) N ( z ) {\displaystyle N(wz)=N(w)N(z)} egyenlőségnek. N kompozíciós tulajdonsága a szorzásra kompozíciós algebrává teszi a ( D , +, ×, * ) testet.

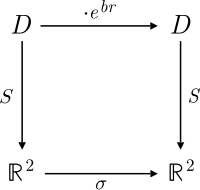
Az R2 vektortér hasonló struktúrát alkot a komponensenkénti műveletekkel és a kvadratikus alakokkal. Ez a struktúra (R2, +, ×, xy), ami kvadratikus tér. A : D → R 2   by   x + y j ↦ ( x + y , x − y ) {\displaystyle D\rightarrow R^{2}\ {\text{by}}\ x+yj\mapsto (x+y,x-y)} gyűrűizomorfizmus arányosan viszonyítja a kvadratikus alakokat, de ez a leképezés nem izometria, mivel R2-ben az (1,1) egység távolsága a nullától √2, ami normalizálva van D -ben.

Definíció

A hasított komplex számok alakja

z = x + j y {\displaystyle z=x+jy}

ahol x és y valós számok, j pedig olyan, hogy

j 2 = + 1 {\displaystyle j^{2}=+1}

és j független a valós számoktól és a komplex számok képzetes egységétől. Az j 2 = − 1 {\displaystyle j^{2}=-1} választás a komplex számokhoz vezet.

Az asszociált bilineáris alak

⟨ z , w ⟩ = Re ⁡ ( z w ∗ ) = Re ⁡ ( z ∗ w ) = x u − y v , {\displaystyle \langle z,w\rangle =\operatorname {Re} (zw^{*})=\operatorname {Re} (z^{*}w)=xu-yv,}

ahol z = x + j y és w = u + j v. A modulus ekvivalens alakja

‖ z ‖ = ⟨ z , z ⟩ . {\displaystyle \lVert z\rVert =\langle z,z\rangle .}

Mivel nem pozitív definit, nem skalárszorzat; ennek ellenére indefinit skalárszorzatnak is nevezik. Egy másik, a matematikai igényességgel össze nem férő szóhasználat normaként hivatkozik a modulusra.

A hasított komplex számok halmazát hasított komplex síknak nevezik. Az összeadás és a szorzás így végezhető:

( x + j y ) + ( u + j v ) = ( x + u ) + j ( y + v ) {\displaystyle (x+jy)+(u+jv)=(x+u)+j(y+v)}
( x + j y ) ( u + j v ) = ( x u + y v ) + j ( x v + y u ) . {\displaystyle (x+jy)(u+jv)=(xu+yv)+j(xv+yu).}

Mindkét művelet kommutatív, asszociatív, és a szorzás disztributív az összeadásra.

Konjugált, modulus, invertálhatóság

Ahogy a komplex számoknál, úgy a hasított komplex számoknál is definiálható a konjugált. A

z = x + j y {\displaystyle z=x+jy}

hasított komplex szám konjugáltja

z ∗ = x − j y . {\displaystyle z^{*}=x-jy.}

Tulajdonságai hasonlítanak a komplex konjugálthoz. Azaz

( z + w ) ∗ = z ∗ + w ∗ {\displaystyle (z+w)^{*}=z^{*}+w^{*}}
( z w ) ∗ = z ∗ w ∗ {\displaystyle (zw)^{*}=z^{*}w^{*}}
( z ∗ ) ∗ = z . {\displaystyle (z^{*})^{*}=z.}

Az z = x + j y hasított komplex szám modulusa az izotropikus kvadratikus alakkal számítható:

‖ z ‖ = z z ∗ = z ∗ z = x 2 − y 2 . {\displaystyle \lVert z\rVert =zz^{*}=z^{*}z=x^{2}-y^{2}.}

Kompozíciós algebra tulajdonsága van:

‖ z w ‖ = ‖ z ‖ ‖ w ‖ . {\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert .}

Ennek szignatúrája (1, −1), ezért nem pozitív definit, így ez nem norma matematikai értelemben.

Egy hasított komplex szám invertálható akkor és csak akkor, ha ( ‖ z ‖ ≠ 0 {\displaystyle \lVert z\rVert \neq 0} ), így az x ± j x alakú hasított komplex számoknak nincs inverze. A nem invertálható elemeket null vektoroknak nevezik. Az invertálható elemek multiplikatív inverze:

z − 1 = z ∗ / ‖ z ‖ . {\displaystyle z^{-1}=z^{*}/\lVert z\rVert .}

Átlós bázis

Az e = (1 − j)/2 és az e∗ = (1 + j)/2 elemek a gyűrű nem triviális idempotens elemei. Ez azt jelenti, hogy ee = e és e∗e∗ = e∗. Mindkét elem null:

‖ e ‖ = ‖ e ∗ ‖ = e ∗ e = 0. {\displaystyle \lVert e\rVert =\lVert e^{*}\rVert =e^{*}e=0.}

Gyakran kényelmes az e és e∗ elemekből alkotott bázist használni. Ennek elnevezése null bázis vagy átlós bázis. Ha z hasított komplex szám, akkor a null bázisban:

z = x + j y = ( x − y ) e + ( x + y ) e ∗ . {\displaystyle z=x+jy=(x-y)e+(x+y)e^{*}.}

Ha az a és a b számokra a z = ae + be∗ számot (a, b) jelöli, akkor a hasított komplex szorzás

( a 1 , b 1 ) ( a 2 , b 2 ) = ( a 1 a 2 , b 1 b 2 ) . {\displaystyle (a_{1},b_{1})(a_{2},b_{2})=(a_{1}a_{2},b_{1}b_{2}).}

Ez a bázis megmutatja, hogy a hasított komplex számok az R ⊕ R vektortérrel gyűrű izomorfizmusban állnak.

A konjugálás eredménye:

( a , b ) ∗ = ( b , a ) {\displaystyle (a,b)^{*}=(b,a)}

és a modulus:

‖ ( a , b ) ‖ = a b . {\displaystyle \lVert (a,b)\rVert =ab.}

Habár a gyűrűknek ugyanabba az izomorfizmusosztályába tartoznak, a hasított komplex sík és a direkt összeg lényegesen különbözik egymástól Az izomorfizmus egy 45 fokos forgatás és egy négyzetgyök kettővel való nyújtás egymásutánja. Ez utóbbi néha zavart okoz a hiperbolaszeletek területének kiszámításában. A hiperbolikus szög megfelel az R ⊕ R {\displaystyle \mathbf {R} \oplus \mathbf {R} } szektorainak területével, ahol { ( a , b ) ∈ R ⊕ R : a b = 1 } . {\displaystyle \lbrace (a,b)\in \mathbf {R} \oplus \mathbf {R} :ab=1\rbrace .} Az összenyomott egységkör, { cosh ⁡ a + j   sinh ⁡ a : a ∈ R } {\displaystyle \lbrace \cosh a+j\ \sinh a:a\in \mathbf {R} \rbrace } területe fele a megfelelő hiperbolikus szektor területének. A zavart csak fokozza, ha nem különböztetik meg a két gyűrű geometriáját.

Geometria

Egységhiperbola, ||z||=1 (kékkel),
konjugált hiperbolája ||z||=−1 (zölddel),
és aszimptotái, ||z||=0 (pirossal)

A kétdimenziós valós vektortér a Minkowski-féle skalárszorzattal ellátva (1 + 1) dimenziós Minkowski-teret alkot, amit gyakran R1,1 jelöl. Ahogy az euklideszi sík, R2 geometriája leírható a komplex számokkal, úgy a Minkowski-tér geometriája, R1,1 leírható a hasított komplex számokkal.

Az

{ z : ‖ z ‖ = a 2 } {\displaystyle \{z:\lVert z\rVert =a^{2}\}}

pontok halmaza hiperbola, minden a eleme R esetén. Jobb és bal ága rendre átmegy a (a, 0) és a (−a, 0) pontokon. Az a = 1 esetben ez az egységhiperbola. A konjugált hiperbola

{ z : ‖ z ‖ = − a 2 } {\displaystyle \{z:\lVert z\rVert =-a^{2}\}}

aminek felső és alsó ága rendre a (0, a) és a (0, −a) pontokon halad át. A hiperbolát és konjugált hiperboláját átlós egyenesek választják el, amelyek null elemekből állnak:

{ z : ‖ z ‖ = 0 } . {\displaystyle \{z:\lVert z\rVert =0\}.}

A két egyenes, amit null kúpnak is neveznek, merőleges R2-ben, és meredekségük ±1.

Ha z és w hasított komplex számok, akkor ortogonálisak, ha <z, w> = 0. Két ortogonális hasított komplex szám bázist alkot.

Az Euler-formulához hasonló formula a hasított komplex számokra is értelmezhető:

exp ⁡ ( j θ ) = ch ⁡ ( θ ) + j sh ⁡ ( θ ) . {\displaystyle \exp(j\theta )=\operatorname {ch} (\theta )+j\operatorname {sh} (\theta ).\,}

Ez származtatható a hatványsorokból, mivel sh hatványsorában csak páratlan, ch hatványsorában csak páros fokú tagok együtthatója különbözik nullától.

Minden θ hiperbolikus szögre a λ = exp(jθ) hasított komplex szám modulusa 1, és az egységhiperbola jobb ágán helyezkedik el. Ezek a 'λ' számok hiperbolikus versorok. A velük való szorzás hiperbolikus forgatásnak felel meg, mivel modulusuk 1. Ez megőrzi a geometriai szerkezetet, hiperbolát hiperbolába visz, és a null kúpot is megőrzi.

A modulust megőrző transzformációk csoportot alkotnak, ez az O(1, 1) általános ortogonális csoport. Ennek részcsoportja SO+(1, 1), ami az 1 modulusú hasított komplex számokkal való szorzást jelenti. Az általános ortogonális csoport ebből úgy kapható, ha bővítünk az

z ↦ ± z {\displaystyle z\mapsto \pm z} és z ↦ ± z ∗ {\displaystyle z\mapsto \pm z^{*}} diszkrét tükrözésekkel.

A z

exp : ( R , + ) → S O + ( 1 , 1 ) {\displaystyle \exp \colon (\mathbb {R} ,+)\to \mathrm {SO} ^{+}(1,1)}

leképezés a θ hasított komplex számot az exp(jθ)-val való forgatásba küldi. Ez csoportizomorfizmus, mivel a szokásos exponenciális formulával:

e j ( θ + ϕ ) = e j θ e j ϕ . {\displaystyle e^{j(\theta +\phi )}=e^{j\theta }e^{j\phi }.\,}

Ha a z hasított komplex szám nem nullelem, akkor z-nek van poláris felbontása.

Algebra

A hasított komplex számok az absztrakt algebrai leírásban az R[x] polinomgyűrű és az x2 − 1 által generált ideál hányadosgyűrűje, R[x]/(x2 − 1).

Ebben a megfeleltetésben az x határozatlan képe a j képzetes egység. Ebben a megfogalmazásban azonnal látható, hogy a hasított komplex számok gyűrűje kommutatív, és karakterisztikája 0. A skalárral szorzást a szokott módon definiálva kétdimenziós asszociatív algebrát kapunk a valós számok fölött. Habár egységelemes, ez a gyűrű nem integritási tartomány vagy test a nullosztók miatt. Mivel az összeadás és a szorzás folytonos a sík szokásos topológiájával, ezért ezzel a topológiával topologikus gyűrűt alkot.

A hasított számok algebrája kompozíciós algebrát alkot, mivel : ‖ z w ‖ = ‖ z ‖ ‖ w ‖ {\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert }  minden z és w hasított komplex számra.

A definíció alapján nyilvánvaló, hogy izomorf az R[C2] gyűrűvel, ahol C2 ciklikus csoport a valós számok fölött.

Mátrixreprezentáció

Kommutatív diagram a hiperbolikus versor hatásával a D gyűrűn a σ leképezésre R2-en

A z = x + j y {\displaystyle z=x+jy} reprezentálható, mint

z ↦ ( x y y x ) . {\displaystyle z\mapsto {\begin{pmatrix}x&y\\y&x\end{pmatrix}}.}

A reprezentációban a műveletek a mátrixokkal végzett műveleteknek felelnek meg. A modulus éppen a mátrix determinánsa. A konjugálás a

C = ( 1 0 0 − 1 ) . {\displaystyle C={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.}

mátrixszal vett kétoldali szorzás.

Bármely valós a számra az a hiperbolikus szöggel való forgatás leírható a

( cosh ⁡ a sinh ⁡ a sinh ⁡ a cosh ⁡ a ) . {\displaystyle {\begin{pmatrix}\cosh a&\sinh a\\\sinh a&\cosh a\end{pmatrix}}.}

mátrixszal végzett szorzással.

Ha a z = x + j y {\displaystyle z=x+jy} hasított komplex számot az (x, y) pár jelzi, akkor az átlós bázisra való áttérés:

( u , v ) = ( x , y ) ( 1 1 1 − 1 ) = ( x , y ) S . {\displaystyle (u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(x,y)S.}

Most a kvadratikus alak u v = ( x + y ) ( x − y ) = x 2 − y 2 . {\displaystyle uv=(x+y)(x-y)=x^{2}-y^{2}.} Továbbá

( cosh ⁡ a , sinh ⁡ a ) ( 1 1 1 − 1 ) = ( e a , e − a ) {\displaystyle (\cosh a,\sinh a){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(e^{a},e^{-a})}

így két paraméterezett hiperbola hozható kapcsolatba S-sel. Így az e b j {\displaystyle e^{bj}\!} hiperbolikus verzor hatása az

σ : ( u , v ) ↦ ( r u , v / r ) , r = e b . {\displaystyle \sigma :(u,v)\mapsto (ru,v/r),\quad r=e^{b}.}

hasonlósági transzformációnak felel meg.

Jegyezzük meg, hogy a hasított komplex számoknak már a 2 x 2-es mátrixok körében is léteznek más reprezentációi. A fenti átlós prezentáció a hasított komplex számok fenti reprezentációja Jordan-normálalakban. A z = (x, y) hasított komplex szám esetén:

Z = ( x y y x ) . {\displaystyle Z={\begin{pmatrix}x&y\\y&x\end{pmatrix}}.}

Jordan-normálalakja:

J z = ( x + y 0 0 x − y ) , {\displaystyle J_{z}={\begin{pmatrix}x+y&0\\0&x-y\end{pmatrix}},}

ahol Z = S J z S − 1   , {\displaystyle Z=SJ_{z}S^{-1}\ ,} és

S = ( 1 − 1 1 1 ) . {\displaystyle S={\begin{pmatrix}1&-1\\1&1\end{pmatrix}}.}

Források

  • Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica delle algebre doppie dotate di modulo", Atti della Reale Accademia delle Scienze e Belle-Lettere di Napoli, Ser (3) v.2 No7. MR0021123.
  • Benz, W. (1973)Vorlesungen uber Geometrie der Algebren, Springer
  • N. A. Borota, E. Flores, and T. J. Osler (2000) "Spacetime numbers the easy way", Mathematics and Computer Education 34: 159-168.
  • N. A. Borota and T. J. Osler (2002) "Functions of a spacetime variable", Mathematics and Computer Education 36: 231-239.
  • K. Carmody, (1988) "Circular and hyperbolic quaternions, octonions, and sedenions", Appl. Math. Comput. 28:47–72.
  • K. Carmody, (1997) "Circular and hyperbolic quaternions, octonions, and sedenions – further results", Appl. Math. Comput. 84:27–48.
  • William Kingdon Clifford,Mathematical Works (1882) edited by A.W.Tucker,pp. 392,"Further Notes on Biquaternions"
  • V.Cruceanu, P. Fortuny & P.M. Gadea (1996) A Survey on Paracomplex Geometry, Rocky Mountain Journal of Mathematics 26(1): 83–115, link from Project Euclid.
  • De Boer, R. (1987) "An also known as list for perplex numbers", American Journal of Physics 55(4):296.
  • Anthony A. Harkin & Joseph B. Harkin (2004) Geometry of Generalized Complex Numbers, Mathematics Magazine 77(2):118–29.
  • F. Reese Harvey. Spinors and calibrations. Academic Press, San Diego. 1990. ISBN 0-12-329650-1. Contains a description of normed algebras in indefinite signature, including the Lorentz numbers.
  • Hazewinkle, M. (1994) "Double and dual numbers", Encyclopaedia of Mathematics, Soviet/AMS/Kluwer, Dordrect.
  • Kevin McCrimmon (2004) A Taste of Jordan Algebras, pp 66, 157, Universitext, Springer ISBN 0-387-95447-3 MR2014924
  • C. Musès, "Applied hypernumbers: Computational concepts", Appl. Math. Comput. 3 (1977) 211–226.
  • C. Musès, "Hypernumbers II—Further concepts and computational applications", Appl. Math. Comput. 4 (1978) 45–66.
  • Olariu, Silviu (2002) Complex Numbers in N Dimensions, Chapter 1: Hyperbolic Complex Numbers in Two Dimensions, pages 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7.
  • Poodiack, Robert D. & Kevin J. LeClair (2009) "Fundamental theorems of algebra for the perplexes", The College Mathematics Journal 40(5):322–35.
  • Isaak Yaglom (1968) Complex Numbers in Geometry, translated by E. Primrose from 1963 Russian original, Academic Press, pp. 18–20.
  • J. Rooney.szerk.: Marco Ceccarelli and Victor A. Glazunov: Generalised Complex Numbers in Mechanics, Advances on Theory and Practice of Robots and Manipulators: Proceedings of Romansy 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. Springer. DOI: 10.1007/978-3-319-07058-2_7 (2014). ISBN 978-3-319-07058-2 

Fordítás

Ez a szócikk részben vagy egészben a Split-complex number című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.