Rozkład logarytmicznie normalny

Rozkład logarytmicznie normalny

Gęstość prawdopodobieństwa µ=0
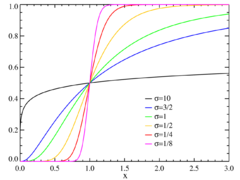
Dystrybuanta µ=0
Parametry	${\displaystyle \sigma >0}$ ${\displaystyle 0\leq \mu <\infty }$
Nośnik	${\displaystyle (0,+\infty )}$
Gęstość prawdopodobieństwa	${\displaystyle {\frac {1}{{\sqrt {2\pi }}\sigma x}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right)\cdot \mathbf {1} _{(0,\infty )}}$
Dystrybuanta	${\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]}$
Wartość oczekiwana (średnia)	${\displaystyle e^{\mu +\sigma ^{2}/2}}$
Mediana	${\displaystyle e^{\mu }}$
Moda	${\displaystyle e^{\mu -\sigma ^{2}}}$
Wariancja	${\displaystyle (e^{\sigma ^{2}}\!\!-1)e^{2\mu +\sigma ^{2}}}$
Współczynnik skośności	${\displaystyle (e^{\sigma ^{2}}\!\!+2){\sqrt {e^{\sigma ^{2}}\!\!-1}}}$
Kurtoza	${\displaystyle {\frac {e^{6\sigma ^{2}}-4e^{3\sigma ^{2}}+6e^{\sigma ^{2}}-3}{e^{4\mu +2\sigma ^{2}}(e^{\sigma ^{2}}-1)^{4}}}}$
Entropia	${\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})+\mu }$
Funkcja tworząca momenty	Nie istnieje funkcja generująca momenty, jednak wszystkie momenty istnieją i są dane wzorem: ${\displaystyle \mu _{k}=e^{k\mu +k^{2}\sigma ^{2}/2}}$
Odkrywca	John Henry Gaddum (1945)

Rozkład logarytmicznie normalny (albo logarytmiczno-normalny, log-normalny) – ciągły rozkład prawdopodobieństwa dodatniej zmiennej losowej, której logarytm ma rozkład normalny.

Z uwagi na to, że wiele zmiennych naturalnie pojawiających się zastosowaniach jest nieujemnych (rozmiar organizmu, wielkość opadów deszczu w meteorologii, przychód w ekonomii), rozkład logarytmicznie normalny znajduje zastosowanie w statystyce. Andriej Kołmogorow wyznaczył rozkład logarytmicznie normalny jako granicę procesu podziału cząsteczki na dwie kolejne o losowych wielkościach^[1]

Definicja

Niech ${\displaystyle X}$ będzie zmienną losową przyjmująca wartości dodatnie. Zmienna ta ma rozkład logarytmicznie normalny z parametrami ${\displaystyle \mu }$ i ${\displaystyle \sigma ^{2},}$ gdy zmienna losowa ${\displaystyle Y=\ln X}$ ma rozkład normalny z parametrami ${\displaystyle \mu }$ i ${\displaystyle \sigma ^{2}.}$ Symbolicznie:

${\displaystyle X\sim \Lambda (\mu ,\sigma ^{2}).}$

Funkcja gęstości zmiennej o rozkładzie ${\displaystyle \Lambda (\mu ,\sigma ^{2})}$ wyraża się wzorem^[2]

${\displaystyle f(x)=\left\{{\begin{array}{ll}{\frac {1}{{\sqrt {2\pi }}\sigma x}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right),&x>0\\0,&x\leqslant 0\end{array}}\right.}$

Przypisy

Bibliografia

• Edwin L. Crow, Kunio Shimizu: Lognormal distributions. Theory and applications. New York: M. Dekker, 1988, seria: Statistics, textbooks and monographs, 88. ISBN 978-0-8247-7803-3. OCLC 949673344. (ang.).