L'Huiliers sats

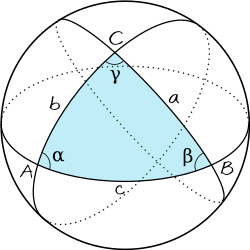
Figur 1.

L'Huiliers sats är en sats inom den sfäriska trigonometrin som säger att det sfäriska överskottet E = α + β + γ − π {\displaystyle E=\alpha +\beta +\gamma -\pi } (beteckningar enligt figur 1) för en sfärisk triangel på en enhetssfär är:[1]

tan ⁡ E 4 = tan ⁡ s 2 ⋅ tan ⁡ s − a 2 ⋅ tan ⁡ s − b 2 ⋅ tan ⁡ s − c 2 {\displaystyle \tan {E \over 4}={\sqrt {\tan {\frac {s}{2}}\cdot \tan {\frac {s-a}{2}}\cdot \tan {\frac {s-b}{2}}\cdot \tan {\frac {s-c}{2}}}}}

där

s = a + b + c 2 {\displaystyle s={\frac {a+b+c}{2}}}

är triangelns semiperimeter (halva omkrets).

Förhållandet, med vars hjälp man kan beräkna en sfärisk triangels area direkt ur dess sidlängder, upptäcktes av den schweiziske matematikern Simon Antoine Jean L'Huilier.

Ett liknande förhållande ges av Cagnolis sats[2] (uppkallad efter den italienske astronomen och matematikern Antonio Cagnoli)

sin ⁡ E 2 = sin ⁡ s ⋅ sin ⁡ ( s − a ) ⋅ sin ⁡ ( s − b ) ⋅ sin ⁡ ( s − c ) 2 ⋅ cos ⁡ a 2 ⋅ cos ⁡ b 2 ⋅ cos ⁡ c 2 {\displaystyle \sin {\frac {E}{2}}={\frac {\sqrt {\sin s\cdot \sin(s-a)\cdot \sin(s-b)\cdot \sin(s-c)}}{2\cdot \cos {\frac {a}{2}}\cdot \cos {\frac {b}{2}}\cdot \cos {\frac {c}{2}}}}}

Härledning

Vi utnyttjar att vi från den plana trigonometrin har

sin ⁡ x − sin ⁡ y cos ⁡ x + cos ⁡ y = 2 cos ⁡ x + y 2 ⋅ 2 sin ⁡ x − y 2 2 cos ⁡ x + y 2 ⋅ 2 cos ⁡ x − y 2 = sin ⁡ x − y 2 cos ⁡ x − y 2 {\displaystyle {\frac {\sin x-\sin y}{\cos x+\cos y}}={\frac {2\cos {\frac {x+y}{2}}\cdot 2\sin {\frac {x-y}{2}}}{2\cos {\frac {x+y}{2}}\cdot 2\cos {\frac {x-y}{2}}}}={\frac {\sin {\frac {x-y}{2}}}{\cos {\frac {x-y}{2}}}}} och med x = α + β {\displaystyle x=\alpha +\beta } och med y = π − γ {\displaystyle y=\pi -\gamma } får vi därför i andra steget:
tan ⁡ E 4 = tan ⁡ α + β + γ − π 4 = = sin ⁡ α + β + γ − π 4 cos ⁡ α + β + γ − π 4 = = sin ⁡ α + β 2 − sin ⁡ π − γ 2 cos ⁡ α + β 2 + cos ⁡ π − γ 2 = = sin ⁡ α + β 2 − cos ⁡ γ 2 cos ⁡ α + β 2 + sin ⁡ γ 2 {\displaystyle {\begin{aligned}\tan {\frac {E}{4}}&=\tan {\frac {\alpha +\beta +\gamma -\pi }{4}}=\\&={\frac {\sin {\frac {\alpha +\beta +\gamma -\pi }{4}}}{\cos {\frac {\alpha +\beta +\gamma -\pi }{4}}}}=\\&={\frac {\sin {\frac {\alpha +\beta }{2}}-\sin {\frac {\pi -\gamma }{2}}}{\cos {\frac {\alpha +\beta }{2}}+\cos {\frac {\pi -\gamma }{2}}}}=\\&={\frac {\sin {\frac {\alpha +\beta }{2}}-\cos {\frac {\gamma }{2}}}{\cos {\frac {\alpha +\beta }{2}}+\sin {\frac {\gamma }{2}}}}\end{aligned}}}

Med hjälp av två av Delambres analogier

sin ⁡ α + β 2 cos ⁡ γ 2 = cos ⁡ a − b 2 cos ⁡ c 2 ⇔ sin ⁡ α + β 2 = cos ⁡ a − b 2 cos ⁡ γ 2 cos ⁡ c 2 {\displaystyle {\frac {\sin {\frac {\alpha +\beta }{2}}}{\cos {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a-b}{2}}}{\cos {\frac {c}{2}}}}\Leftrightarrow \sin {\frac {\alpha +\beta }{2}}={\frac {\cos {\frac {a-b}{2}}\cos {\frac {\gamma }{2}}}{\cos {\frac {c}{2}}}}} och cos ⁡ α + β 2 sin ⁡ γ 2 = cos ⁡ a + b 2 cos ⁡ c 2 ⇔ cos ⁡ α + β 2 = cos ⁡ a + b 2 sin ⁡ γ 2 cos ⁡ c 2 {\displaystyle {\frac {\cos {\frac {\alpha +\beta }{2}}}{\sin {\frac {\gamma }{2}}}}={\frac {\cos {\frac {a+b}{2}}}{\cos {\frac {c}{2}}}}\Leftrightarrow \cos {\frac {\alpha +\beta }{2}}={\frac {\cos {\frac {a+b}{2}}\sin {\frac {\gamma }{2}}}{\cos {\frac {c}{2}}}}} får vi
tan ⁡ E 4 = cos ⁡ a − b 2 ⋅ cos ⁡ γ 2 cos ⁡ c 2 − cos ⁡ γ 2 cos ⁡ a + b 2 ⋅ sin ⁡ γ 2 cos ⁡ c 2 + sin ⁡ γ 2 = = cos ⁡ a − b 2 cos ⁡ γ 2 − cos ⁡ c 2 ⋅ cos ⁡ γ 2 cos ⁡ a + b 2 sin ⁡ γ 2 + cos ⁡ c 2 ⋅ sin ⁡ γ 2 = = cos ⁡ a − b 2 − cos ⁡ c 2 cos ⁡ a + b 2 + cos ⁡ c 2 ⋅ cos ⁡ γ 2 sin ⁡ γ 2 = sin ⁡ a − b + c 4 ⋅ sin ⁡ c − a + b 4 cos ⁡ a + b + c 4 ⋅ cos ⁡ a + b − c 4 ⋅ cot ⁡ γ 2 {\displaystyle {\begin{aligned}\tan {\frac {E}{4}}&={\frac {{\frac {\cos {\frac {a-b}{2}}\cdot \cos {\frac {\gamma }{2}}}{\cos {\frac {c}{2}}}}-\cos {\frac {\gamma }{2}}}{{\frac {\cos {\frac {a+b}{2}}\cdot \sin {\frac {\gamma }{2}}}{\cos {\frac {c}{2}}}}+\sin {\frac {\gamma }{2}}}}=\\&={\frac {\cos {\frac {a-b}{2}}\cos {\frac {\gamma }{2}}-\cos {\frac {c}{2}}\cdot \cos {\frac {\gamma }{2}}}{\cos {\frac {a+b}{2}}\sin {\frac {\gamma }{2}}+\cos {\frac {c}{2}}\cdot \sin {\frac {\gamma }{2}}}}=\\&={\frac {\cos {\frac {a-b}{2}}-\cos {\frac {c}{2}}}{\cos {\frac {a+b}{2}}+\cos {\frac {c}{2}}}}\cdot {\frac {\cos {\frac {\gamma }{2}}}{\sin {\frac {\gamma }{2}}}}\\&={\frac {\sin {\frac {a-b+c}{4}}\cdot \sin {\frac {c-a+b}{4}}}{\cos {\frac {a+b+c}{4}}\cdot \cos {\frac {a+b-c}{4}}}}\cdot \cot {\frac {\gamma }{2}}\end{aligned}}}

Där vi i sista steget utnyttjade cos ⁡ x − cos ⁡ y = − sin ⁡ x + y 2 ⋅ sin ⁡ x − y 2 = sin ⁡ x + y 2 ⋅ sin ⁡ y − x 2 {\displaystyle \cos x-\cos y=-\sin {\frac {x+y}{2}}\cdot \sin {\frac {x-y}{2}}=\sin {\frac {x+y}{2}}\cdot \sin {\frac {y-x}{2}}} och cos ⁡ x + cos ⁡ y = cos ⁡ x + y 2 ⋅ cos ⁡ x − y 2 {\displaystyle \cos x+\cos y=\cos {\frac {x+y}{2}}\cdot \cos {\frac {x-y}{2}}} .

Vi inför nu s = a + b + c 2 {\displaystyle s={\frac {a+b+c}{2}}} och tar hjälp av den sfäriska formeln för cotangens för halva vinkeln, cot ⁡ γ 2 = sin ⁡ s ⋅ sin ⁡ ( s − c ) sin ⁡ ( s − a ) ⋅ sin ⁡ ( s − b ) {\displaystyle \cot {\frac {\gamma }{2}}={\sqrt {\frac {\sin s\cdot \sin(s-c)}{\sin(s-a)\cdot \sin(s-b)}}}} och sedan av den plantrigonometriska sin ⁡ x = 2 sin ⁡ x 2 cos ⁡ x 2 {\displaystyle \sin x=2\sin {\frac {x}{2}}\cos {\frac {x}{2}}} , vilket ger

tan ⁡ E 4 = sin ⁡ s − b 2 ⋅ sin ⁡ s − a 2 cos ⁡ s 2 ⋅ cos ⁡ s − c 2 ⋅ sin ⁡ s ⋅ sin ⁡ ( s − c ) sin ⁡ ( s − a ) ⋅ sin ⁡ ( s − b ) = = sin ⁡ s − b 2 ⋅ sin ⁡ s − a 2 cos ⁡ s 2 ⋅ cos ⁡ s − c 2 ⋅ 2 sin ⁡ s 2 ⋅ cos ⁡ s 2 ⋅ 2 sin ⁡ s − c 2 ⋅ cos ⁡ s − c 2 2 sin ⁡ s − a 2 ⋅ cos ⁡ s − a 2 ⋅ 2 sin ⁡ s − b 2 ⋅ cos ⁡ s − b 2 = = sin 2 ⁡ s − b 2 ⋅ sin 2 ⁡ s − a 2 ⋅ sin ⁡ s 2 ⋅ cos ⁡ s 2 ⋅ sin ⁡ s − c 2 ⋅ cos ⁡ s − c 2 cos 2 ⁡ s 2 ⋅ cos 2 ⁡ s − c 2 ⋅ sin ⁡ s − a 2 ⋅ cos ⁡ s − a 2 ⋅ sin ⁡ s − b 2 ⋅ cos ⁡ s − b 2 = = sin ⁡ s 2 ⋅ sin ⁡ s − a 2 ⋅ sin ⁡ s − b 2 ⋅ sin ⁡ s − c 2 cos ⁡ s 2 ⋅ cos ⁡ s − a 2 ⋅ cos ⁡ s − b 2 ⋅ cos ⁡ s − c 2 = = tan ⁡ s 2 ⋅ tan ⁡ s − a 2 ⋅ tan ⁡ s − b 2 ⋅ tan ⁡ s − c 2 Q . E . D . {\displaystyle {\begin{aligned}\tan {\frac {E}{4}}&={\frac {\sin {\frac {s-b}{2}}\cdot \sin {\frac {s-a}{2}}}{\cos {\frac {s}{2}}\cdot \cos {\frac {s-c}{2}}}}\cdot {\sqrt {\frac {\sin s\cdot \sin(s-c)}{\sin(s-a)\cdot \sin(s-b)}}}=\\&={\frac {\sin {\frac {s-b}{2}}\cdot \sin {\frac {s-a}{2}}}{\cos {\frac {s}{2}}\cdot \cos {\frac {s-c}{2}}}}\cdot {\sqrt {\frac {2\sin {\frac {s}{2}}\cdot \cos {\frac {s}{2}}\cdot 2\sin {\frac {s-c}{2}}\cdot \cos {\frac {s-c}{2}}}{2\sin {\frac {s-a}{2}}\cdot \cos {\frac {s-a}{2}}\cdot 2\sin {\frac {s-b}{2}}\cdot \cos {\frac {s-b}{2}}}}}=\\&={\sqrt {\frac {\sin ^{2}{\frac {s-b}{2}}\cdot \sin ^{2}{\frac {s-a}{2}}\cdot \sin {\frac {s}{2}}\cdot \cos {\frac {s}{2}}\cdot \sin {\frac {s-c}{2}}\cdot \cos {\frac {s-c}{2}}}{\cos ^{2}{\frac {s}{2}}\cdot \cos ^{2}{\frac {s-c}{2}}\cdot \sin {\frac {s-a}{2}}\cdot \cos {\frac {s-a}{2}}\cdot \sin {\frac {s-b}{2}}\cdot \cos {\frac {s-b}{2}}}}}=\\&={\sqrt {\frac {\sin {\frac {s}{2}}\cdot \sin {\frac {s-a}{2}}\cdot \sin {\frac {s-b}{2}}\cdot \sin {\frac {s-c}{2}}}{\cos {\frac {s}{2}}\cdot \cos {\frac {s-a}{2}}\cdot \cos {\frac {s-b}{2}}\cdot \cos {\frac {s-c}{2}}}}}=\\&={\sqrt {\tan {\frac {s}{2}}\cdot \tan {\frac {s-a}{2}}\cdot \tan {\frac {s-b}{2}}\cdot \tan {\frac {s-c}{2}}}}\qquad Q.E.D.\end{aligned}}}

Referenser

  • Isaac Todhunter, 1886, Spherical Trigonometry: For the Use of Colleges and Schools, Macmillan & Co. Faksimil PDF (3 MB), TeX PDF (789 kB). 1883 års upplaga online på Google Books. L'Huiliers sats behandlas i artikel 102 på sid.70.
  • John Casey, 1889, A Treatise on Spherical Trigonometry, and Its Application to Geodesy and Astronomy, with Numerous Examples, Dublin, Hodges, Figgis, & co. Online på Archive.org. PDF (5,5 MB). Se artiklarna 46-48, sid. 43-44 och kapitel 5, sid. 85 ff.
  1. ^ Eric W. Weisstein, L'Huiliers Theorem på Wolfram MathWorld.
  2. ^ Todhunter (1886), artikel 101, sid. 70.